Nakita.id - Mata pelajaran Matematika kelas 11 SMA peminatan Kurikulum Merdeka tengah membahas bab 3.
Adapun materi yang dibahas dalam bab 3 Matematika kelas 11 SMA Kurikulum Merdeka adalah tentang irisan kerucut.
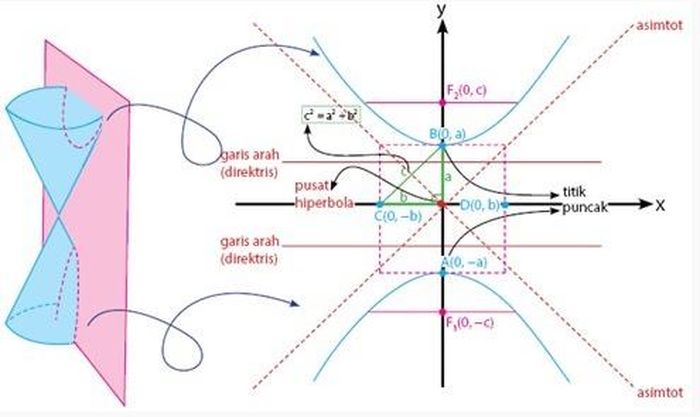
Pada artikel Kurikulum Merdeka sebelumnya, telah dijelaskan bahwa ada beberapa bentuk irisan, yaitu lingkaran, parabola, elips, dan hiperbola.
Kali ini, kita akan membahas bentuk terakhir irisan kerucut, yaitu hiperbola. Berikut ini materi hiperbola sebagai salah satu bentuk irisan kerucut.
Hiperbola didefinisikan sebagai kedudukan titik-titik yang selisih jaraknya dari dua titik (titik fokus) adalah konstan.
Persamaan hiperbola dengan titik pusat (0,0) dan (h,k) adalah sebagai berikut:
Persamaan garis singgung hiperbola yang melalui titik (x1, y1) adalah:
Persamaan hiperbola Persamaan garis singgung
Baca Juga: Elips sebagai Bentuk Irisan Kerucut, Materi Lengkap Bab 3 Matematika Kelas 11 SMA Kurikulum Merdeka
x2/a2 - y2/b2 = 1 x1x/a2 - y1y/b2 = 1
x2/b2 - y2/a2 = 1 x1x/b2 - y1y/a2 = 1
(x – h)2/a2 - (y – k)2/b2 = 1 (x1 – h)(x – h)/a2 - (y1 – k)(y– k)/b2 = 1
(y – k)2/b2 - (x – h)2/a2 = 1 (y1 – k)(y – k)/a2 - (x1 – h)(x– h)/b2 = 1
Persamaan garis singgung hiperbola dengan gradien m pada elips adalah:
Persamaan hiperbola Persamaan garis singgung
x2/a2 - y2/b2 = 1 y = mx ± √a2m2 - b2
x2/b2 - y2/a2 = 1 y = mx ± √a2 - b2m2
(x – h)2/a2 - (y – k)2/b2 = 1 y – k = m(x – h) ± √a2m2 - b2
(y – k)2/a2 - (x – h)2/b2 = 1 y – k = m(x – h) ± √a2 - b2m2
Nah, itu dia materi bab 3 Matematika kelas 11 SMA Kurikulum Merdeka tentang hiperbola sebagai salah satu bentuk irisan kerucut. Semoga bermanfaat!
ShopTokopedia dan Tasya Farasya Luncurkan Kampanye ‘Semua Jadi Syantik’, Rayakan Kecantikan yang Inklusif
| Penulis | : | Ratnaningtyas Winahyu |
| Editor | : | Ratnaningtyas Winahyu |
KOMENTAR