Bentuk Polar dan Eksponen Bilangan Kompleks, Jawaban Latihan A Halaman 14 Matematika Tingkat Lanjut Kelas XI SMA Kurikulum Merdeka

Nakita.id – Saat ini, kita sedang membahas mata pelajaran Matematika Tingkat Lanjut kelas XI SMA Kurikulum Merdeka bab 1.

Materi yang dijelaskan dalam bab 1 ini adalah tentang bilangan kompleks.

Pada artikel Kurikulum Merdeka sebelumnya, kita telah membahas pengertian bilangan kompleks.

Sekarang, kita akan membahas bentuk-bentuknya.

Bentuk polar bilangan kompleks

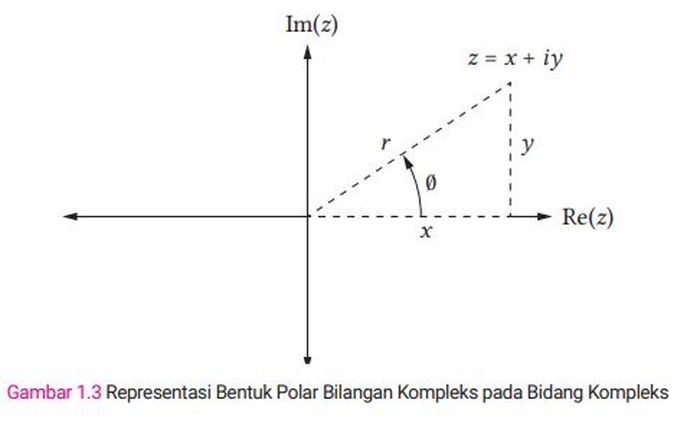
Misalkan x, y bilangan real maka bilangan kompleks z = x + iy dapat dinyatakan dalam bentuk polar yakni,

z = r(cosθ + isinθ) dengan r = √x² + y² , x = r cos θ dan y = r sin θ.

Untuk menyatakan bilangan kompleks dalam bentuk polar, perhatikan ilustrasi gambar berikut.

Bentuk eksponen bilangan kompleks

Selain itu, terdapat suatu identitas yang menyatakan e^iθ = cosθ + isinθ.

Dengan memanfaatkan identitas tersebut, maka bilangan kompleks z = r(cosθ + isinθ) bisa dinyatakan dalam bentuk z = r(cosθ + isinθ) = re^iθ.

Bentuk bilangan kompleks z = re^iθ  disebut sebagai bentuk eksponen.

Baca Juga: Pengertian Bilang Kompleks dan Bentuk-bentuknya, Materi Bab 1 Matematika Tingkat Lanjut Kelas XI SMA Kurikulum Merdeka

Adapun definisi bentuk eksponen bilangan kompleks dinyatakan sebagai berikut.

Misalkan z = r(cosθ + isinθ) adalah bentuk polar bilangan kompleks.

Maka, z dapat dinyatakan dalam bentuk eksponen, yakni:

bilangan real maka bilangan kompleks z = x + iy dapat dinyatakan dalam bentuk polar yakni,

z = re^iθ  

dengan e^iθ = cos θ + isin θ.

Agar lebih mudah memahami konsep bentuk bilangan kompleks, yuk kita langsung isi Latihan A halaman 14 buku Matematika Tingkat Lanjut kelas XI SMA Kurikulum Merdeka.

Latihan A

Pemahaman konsep

1. Benar atau salah. Setiap bilangan real adalah bilangan kompleks.

2. Benar atau salah. Bilangan kompleks mempunyai 3 bentuk yakni bentuk kartesius, bentuk eksponen, dan bentuk logaritma.

Baca Juga: Terlengkap, Rangkuman Bab 3 Statistika Matematika Kelas XI SMA Kurikulum Merdeka

3. Benar atau salah. Bilangan kompleks z = 1 – 3i jika digambarkan pada bidang kompleks, maka berada di kuadran III.

Penerapan konsep

4. Nyatakan bilangan kompleks 2 + 2i dalam bentuk polar dan eksponen.

5. Tentukan bilangan x dan y dengan z₁ = x + 3i dan z₂ = 3 – yi agar z₁ = z₂!

6. Tentukan solusi dari persamaan kuadrat x² – 2x + 6 = 0!

7. Tentukan persamaan kuadrat yang mempunyai solusi x₁ = 1 + i dan z₂ = 1 – i!

Jawaban

1) Benar

2) Salah

3) Salah

4) Perhatikan bahwa, bilangan kompleks z = 2 + 2i mempunyai r = √2² + 2² = √8 = 2 √2.

Baca Juga: Kunci Jawaban Soal Statistika Uji Kompetensi Halaman 125 Nomor 8-10 Matematika Kelas XI SMA Kurikulum Merdeka

Dan, sin θ = 1/√2 dan cos θ = 1/√2.

Salah satu nilai θ yang memenuhi adalah θ = 45º.

Jadi, bentuk polar dari bilangan kompleks z = 2 + 2i adalah z = 2/√2 (cos 45º + i sin 45º).

Sedangkan, bentuk eksponen dari z = 2/√2 (cos 45º + i sin 45º) adalah z = 2/√2 e^i45º.

5) Nilai x dan y yang memenuhi adalah x = 3 dan y = -3.

6) Solusi persamaan kuadrat x² – 2x + 6 = 0

(Gambar)

7) Persamaan kuadrat yang mempunyai solusi x₁ dan x₂  adalah x² – (x₁ + x₂) x + x₁ x₂ = 0.

Jadi, persamaan kuadrat yang mempunyai akar-akar x₁ = 1 + i dan x₂ = 1 + i   adalah x² – ((1 + i) + (1 – i)) x + (1 + i) (1 + i)  = 0 atau  x² – 2x + 2 = 0.

Nah, itu dia jawaban Latihan A halaman 14 buku Matematika Tingkat Lanjut kelas XI SMA Kurikulum Merdeka.

Semoga bermanfaat!

Baca Juga: Jawaban Soal Statistika Uji Kompetensi Halaman 125 Nomor 4-7 Buku Matematika Kelas XI SMA Kurikulum Merdeka

PROMOTED CONTENT