a) Luas tanah yang diperlukan untuk membangun rumah tipe A dan tipe B di atas tanah seluas 10.000m2 ditentukan oleh pertidaksamaan: 100x + 75y ≤ 10.000, pertidaksamaan ini disederhanakan menjadi: 4x + 3y ≤ 400
b) Jumlah rumah yang akan dibangun x + y ≤ 125
Dari pertidaksamaan (1) dan (2)), kita tentukan banyak rumah tipe A dan tipe B yang dapat dibangun dengan menerapkan metode eliminasi pada sistem persamaan linear dua variabel berikut.
Dengan demikian, Pak Rendi dapat membangun rumah tipe A sebanyak 25 unit, dan rumah tipe B sebanyak 100 unit.
2) Grafik daerah penyelesaian pada diagram kartesius
Untuk menggambar daerah penyelesaian pada diagram kartesius dilakukan langkah-langkah sebagai berikut.
Langkah 1 : Menggambar garis dengan persamaan 4x + 3y = 400 dan garis x + y = 125.
Agar kita mudah menggambar garis ini, terlebih dahulu kita cari titik potong dengan sumbu x yang terjadi jika y = 0 dan titik potong dengan sumbu y yang terjadi jika x = 0.
Untuk garis 4x + 3y = 400, jika y = 0, maka x = 100. jika x = 0, maka y = 133,3.
Maka garis 4x + 3y = 400 memotong sumbu y di titik (0, 133,3) dan memotong sumbu y di titik (100, 0).
Baca Juga: Ketahui Rumus Keliling dan Luas Trapesium di Sini, Catat Sekarang!
| Penulis | : | Syifa Amalia |
| Editor | : | Ratnaningtyas Winahyu |

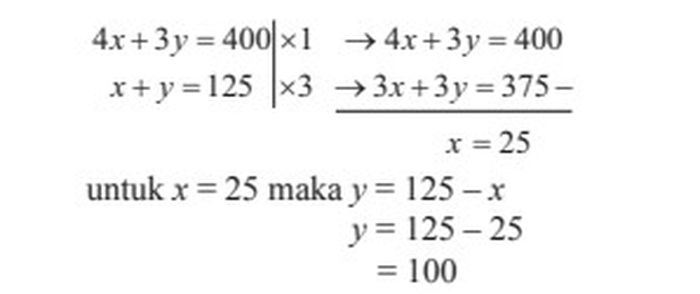
KOMENTAR