Untuk garis x + y = 125, jika y = 0 maka x = 125 jika x = 0 maka y = 125
Maka gari x + y = 125 memotong sumbu y di titik (0,125) dan memotong sumbu x di titik (125, 0).
Langkah 2 : Menentukan daerah penyelesaian pertidaksamaan 4x + 3y ≤ 400 dan x + y ≤ 125.
Daerah penyelesaian pertidaksamaan 4x + 3y ≤ 400. Jika garis 4x + 3y = 400 digambar pada diagram kartesius maka garis tersebut akan membagi dua daerah, yaitu daerah 4x + 3y < 400 dan daerah 4x + 3y > 400.
Selanjutnya menyelidiki daerah mana yang menjadi daerah penyelesaian dari pertidaksamaan 4x + 3y ≤ 400, dengan cara mengambil sebarang titik misal P(x,y) pada salah satu daerah, kemudian mensubstitusikan titik tersebut ke pertidaksamaan 4x + 3y ≤ 400.
Jika pertidaksamaan tersebut bernilai benar maka daerah yang memuat titik P(x,y) merupakan daerah penyelesaiannya, jika bernilai salah maka daerah tersebut bukan daerah penyelesaian pertidaksamaan 4x + 3y ≤ 400.
Dengan cara yang sama maka daerah penyelesaian pertidaksamaan x + y ≤ 125 juga dapat diketahui.
Langkah 3 : Mengarsir daerah yang merupakan daerah penyelesaian masing-masing pertidaksamaan.
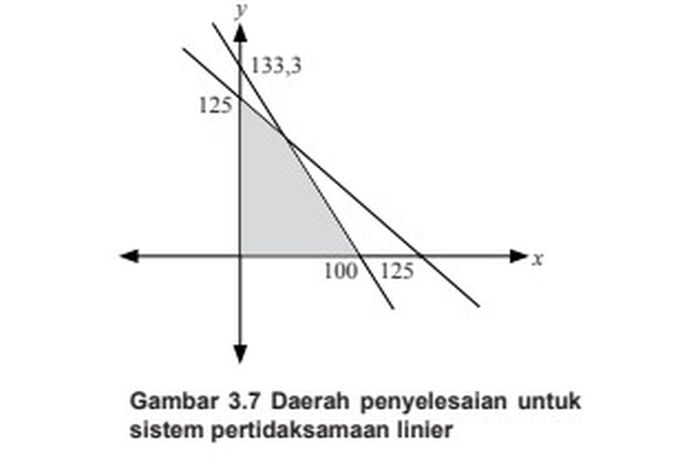
Daerah yang diarsir dua kali merupakan daerah penyelesaian dari sistem pertidaksamaan linier. Setelah langkah 1, 2, dan 3 di atas dilakukan, maka daerah penyelesaian sistem pertidaksamaan digambarkan sebagai berikut.
Nah, itu dia adalah penjelasan mengenai pertidaksamaan linear dua variabel dan contoh soalnya.
Baca Juga: Rumus Keliling dan Luas Lingkaran Beserta Contoh Pengerjaan
| Penulis | : | Syifa Amalia |
| Editor | : | Ratnaningtyas Winahyu |

KOMENTAR