Nakita.id – Dalam pelajaran matematika sekolah menengah, materi yang hampir selalu ada adalah mengenai pertidaksamaan linear dua variabel.
Sering kali, materi mengenai pertidaksamaan linear dua variabel kerap membingungkan siswa.
Mereka memerlukan pemahaman lebih lanjut untuk menguasai dan mampu menyelesaikan soal mengenai pertidaksamaan linear dua variabel.
Karena kerap muncul dalam pelajaran matematika, pasti sudah tidak asing dengan materi ini.
Apa itu pertidaksamaan linear dua variabel?
Pertidaksamaan linear dua variabel memuat dua variabel berpangkat satu yang membuat tanda ketidaksamaan.
Tanda ketidaksamaan ini diantaranya ialah kurang dari (<), lebih dari (>), kurang dari sama dengan (≤) dan lebih dari sama dengan (≥).
Pada umumnya, variabel ditulis sebagai variabel x dan variabel y.
Bentuk umum pertidaksamaan dua variabel di antaranya :
1. ax+byc
2. ax+by≤c, atau
Baca Juga: Referensi Contoh Soal dan Pembahasan Luas dan Keliling Lingkaran
3. ax+by≥c
Langkah menentukan daerah penyelesaian pertidaksamaan linear dua variabel jika diketahui pertidaksamaan linearnya:
Memperhatikan bentuk pertidaksamaan linear dua variabel
Membuat garis pada bidang cartesius, dengan cara:
- Membuat titik potong pada sumbu y dengan cara mensubstitusi x=0 ke dalam persamaan.
- Membuat titik potong pada sumbu x dengan cara mensubstitusi y=0 ke dalam persamaan.
- Membuat garis yang melalui titik potong sumbu x dan y yang telah ditentukan
Menentukan daerah penyelesaian dengan cara menguji pada sembarang titik (a,b) yang berada di luar persamaan garis. Jika pertidaksamaan yang dihasilkan bernilai benar, maka daerah tersebut merupakan daerah penyelesaian. Jika bernilai salah, maka daerah di seberang garis lah yang merupakan daerah penyelesaiannya.
Membuat arsiran pada daerah penyelesaiannya sebagai tanda.
Langkah menentukan pertidaksamaan linear dua variabel jika diketahui daerah penyelesaian:
- Tentukan persamaan garisnya
Baca Juga: Rumus Luas dan Keliling Jajar Genjang, Juga Contoh Soal dan Pembahasannya
- Jika garis melalui koordinat (0,m) dan (n,0), maka persamaan garisnya mx+ny=mn-
- Jika garis melalui titik (x1, y1) dan (x2,y2), maka rumus persamaan garisnya:
Menentukan tanda pertidaksamaan dengan cara membuat titik uji pada sembaran titik (a,b) yang berada di luar persamaan garis.
Pak Rendi berencana membangun 2 tipe rumah; yaitu, tipe A dan tipe B di atas sebidang tanah seluas 10.000 m2 .
Setelah dia berkonsultasi dengan arsitek, ternyata untuk membangun sebuah rumah tipe A dibutuhkan tanah seluas 100 m2 dan untuk membangun sebuah rumah tipe B dibutuhkan tanah seluas 75 m2 .
Karena dana yang dimilikinya terbatas, maka banyak rumah yang direncanakan akan dibangun paling banyak 125 unit. Jika kamu adalah arsitek Pak Rendi,
1) bantulah Pak Rendi menentukan berapa banyak rumah tipe A dan tipe B yang mungkin dapat dibangun sesuai dengan kondisi luas tanah yang ada dan jumlah rumah yang akan dibangun
2) gambarkanlah daerah penyelesaian pada bidang kartesius berdasarkan batasan-batasan yang telah diuraikan.
Penyelesaian:
Diketahui x: banyak rumah tipe A yang akan dibangun dan y: banyak rumah tipe B yang akan dibangun
1) Banyak rumah tipe A dan tipe B yang dapat dibangun
Baca Juga: Berperan Sama Mengajarkan Anak Matematika, Dads Bisa Lakukan 4 Cara Ini Agar Lebih Menyenangkan
a) Luas tanah yang diperlukan untuk membangun rumah tipe A dan tipe B di atas tanah seluas 10.000m2 ditentukan oleh pertidaksamaan: 100x + 75y ≤ 10.000, pertidaksamaan ini disederhanakan menjadi: 4x + 3y ≤ 400
b) Jumlah rumah yang akan dibangun x + y ≤ 125
Dari pertidaksamaan (1) dan (2)), kita tentukan banyak rumah tipe A dan tipe B yang dapat dibangun dengan menerapkan metode eliminasi pada sistem persamaan linear dua variabel berikut.
Dengan demikian, Pak Rendi dapat membangun rumah tipe A sebanyak 25 unit, dan rumah tipe B sebanyak 100 unit.
2) Grafik daerah penyelesaian pada diagram kartesius
Untuk menggambar daerah penyelesaian pada diagram kartesius dilakukan langkah-langkah sebagai berikut.
Langkah 1 : Menggambar garis dengan persamaan 4x + 3y = 400 dan garis x + y = 125.
Agar kita mudah menggambar garis ini, terlebih dahulu kita cari titik potong dengan sumbu x yang terjadi jika y = 0 dan titik potong dengan sumbu y yang terjadi jika x = 0.
Untuk garis 4x + 3y = 400, jika y = 0, maka x = 100. jika x = 0, maka y = 133,3.
Maka garis 4x + 3y = 400 memotong sumbu y di titik (0, 133,3) dan memotong sumbu y di titik (100, 0).
Baca Juga: Ketahui Rumus Keliling dan Luas Trapesium di Sini, Catat Sekarang!
Untuk garis x + y = 125, jika y = 0 maka x = 125 jika x = 0 maka y = 125
Maka gari x + y = 125 memotong sumbu y di titik (0,125) dan memotong sumbu x di titik (125, 0).
Langkah 2 : Menentukan daerah penyelesaian pertidaksamaan 4x + 3y ≤ 400 dan x + y ≤ 125.
Daerah penyelesaian pertidaksamaan 4x + 3y ≤ 400. Jika garis 4x + 3y = 400 digambar pada diagram kartesius maka garis tersebut akan membagi dua daerah, yaitu daerah 4x + 3y < 400 dan daerah 4x + 3y > 400.
Selanjutnya menyelidiki daerah mana yang menjadi daerah penyelesaian dari pertidaksamaan 4x + 3y ≤ 400, dengan cara mengambil sebarang titik misal P(x,y) pada salah satu daerah, kemudian mensubstitusikan titik tersebut ke pertidaksamaan 4x + 3y ≤ 400.
Jika pertidaksamaan tersebut bernilai benar maka daerah yang memuat titik P(x,y) merupakan daerah penyelesaiannya, jika bernilai salah maka daerah tersebut bukan daerah penyelesaian pertidaksamaan 4x + 3y ≤ 400.
Dengan cara yang sama maka daerah penyelesaian pertidaksamaan x + y ≤ 125 juga dapat diketahui.
Langkah 3 : Mengarsir daerah yang merupakan daerah penyelesaian masing-masing pertidaksamaan.
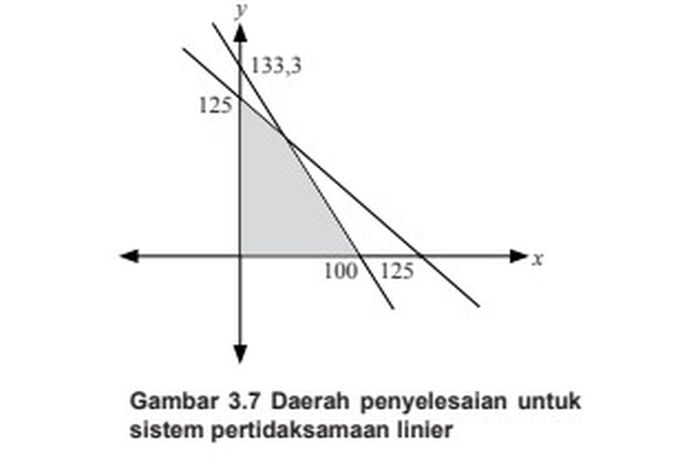
Daerah yang diarsir dua kali merupakan daerah penyelesaian dari sistem pertidaksamaan linier. Setelah langkah 1, 2, dan 3 di atas dilakukan, maka daerah penyelesaian sistem pertidaksamaan digambarkan sebagai berikut.
Nah, itu dia adalah penjelasan mengenai pertidaksamaan linear dua variabel dan contoh soalnya.
Baca Juga: Rumus Keliling dan Luas Lingkaran Beserta Contoh Pengerjaan
| Penulis | : | Syifa Amalia |
| Editor | : | Ratnaningtyas Winahyu |

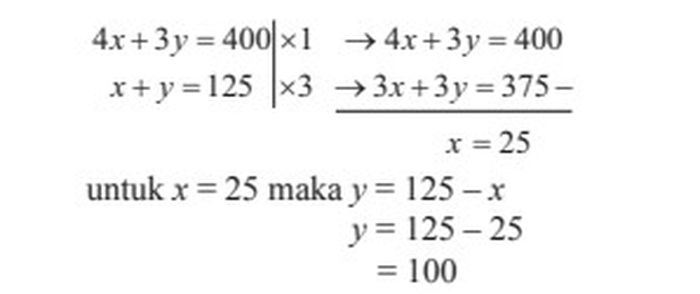
KOMENTAR