Nakita.id – Saat ini, materi yang dipelajari dalam mata pelajaran Matematika Tingkat Lanjut kelas XI SMA Kurikulum Merdeka masih pada bab 3.
Setelah selesai membahas subbab perkalian matriks, kini kita berlanjut ke determinan dan invers matriks.
Sebelum kita mengerjakan soal-soalnya, yuk kita bahas mengenai determinan matriks terlebih dahulu.
Definisi determinan matriks adalah jika A =
Maka determinan dari matriks A dapat dinyatakan:
det A = |A| =
Konsep determinan matriks ada kaitannya dengan penyelesaian sistem persamaan linear. Kita perhatikan sistem persamaan linear dua variabel (SPLDV) berikut.
Solusi umum dari sistem persamaan linear dua variabel (SPLDV) tersebut dapat ditunjukkan berikut ini.
Perhatikan bahwa kedua pecahan sebelumnya memiliki penyebut yang sama yaitu a11a22 - a21a12 yang disebut sebagai determinan matriks A. Dari definisi determinan matriks, penyelesaian sistem persamaan linear dua variabel (SPLDV) dapat ditentukan dengan menggunakan matriks sebagai berikut.
Nilai x dan y dapat ditentukan:
Himpunan penyelesaian sistem persamaan linear dua variabel (SPLDV) adalah himpunan yang memuat pasangan berurutan (x , y).
Untuk menentukan determinan matriks berordo 3×3 dengan metode Sarrus, caranya adalah dengan menyalin elemen-elemen pada kolom pertama dan kedua dari matriks tersebut ke sebelah kanan.
Setelah itu, determinan matriks berordo 3×3 diperoleh dengan menjumlahkan atau mengurangkan dari hasil perhitungan enam diagonal (elemen tiap diagonal dikalikan dahulu), seperti yang ditunjukkan berikut ini.
Misalnya A =
Maka, determinan matriks A:
Catatan: Metode Sarrus hanya dapat digunakan untuk menentukan determinan matriks berordo 2×2 dan 3×3.
Metode ekspansi kofaktor digunakan untuk menentukan determinan berordo lebih dari 2×2.
Jika A adalah sebuah matriks persegi maka minor elemen aij dinotasikan Mij dan didefinisikan sebagai determinan dari sebuah matriks yang diperoleh setelah baris ke-i dan kolom ke-j matriks A dihilangkan.
Kofaktor elemen baris ke-i dan kolom ke-j adalah kij = (-1)i+jMij. Untuk memahami minor dan kofaktor, perhatikan penjelasan berikut. Misalkan A adalah matriks berordo 3×3, minor a22 diperoleh dengan menghilangkan elemen pada baris kedua dan kolom kedua.
Jika A adalah sebuah matriks persegi (ordo lebih dari 2×2), maka determinan matriks A dapat ditentukan sebagai berikut.
Jika |A| dan |B|, maka |AB| = |A||B|.
Nah, itu dia penjelasan mengenai determinan dan invers matriks bab 3 Matematika Tingkat Lanjut kelas XI SMA Kurikulum Merdeka. Semoga bermanfaat!

Rekomendasi Sunscreen untuk Si Kecil: Gently Sunscreen SPF50+ PA++++ dengan Serum Anti-Polusi!

| Penulis | : | Ratnaningtyas Winahyu |
| Editor | : | Ratnaningtyas Winahyu |










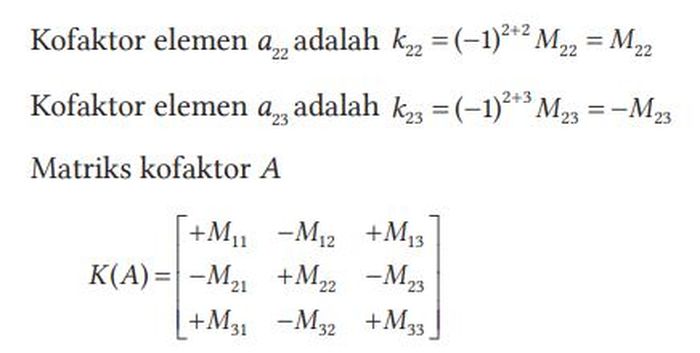

KOMENTAR