Komposisi Fungsi dan Invers Fungsi Buku Kurmer Matematika SMA Kelas XI

Jika f(x) dan g(x) merupakan dua fungsi dengan domain masing-masing D_f dan D_g. Maka, perkalian (f · g)(x) = f(x) · g(x) menghasilkan fungsi yang baru dengan domain D_f ∩ D_g.

Pembagian dua fungsi (f/g) (x) = f(x)/g(x) secara umum belum tentu menghasilkan fungsi. Supaya f/g menjadi sebuah fungsi, pembagi g tidak boleh memiliki nilai 0. Dengan kata lain, f/g adalah fungsi dengan domain (D_f ∩ D_g) – {x|g (x) = 0}.

Komposisi fungsi

Definisi komposisi fungsi

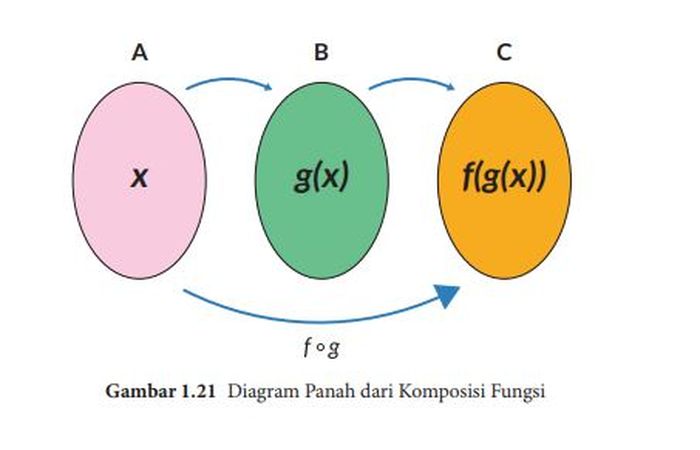
Jika g : A → B dan f : B → C merupakan dua fungsi, maka komposisi keduanya f (g (x)) dinyatakan dengan notasi (f ◦ g)(x) adalah fungsi dari domain A ke kodomain C.

Komposisi dua fungsi dapat dipahami melalui diagram panah berikut:

Syarat komposisi fungsi

Dua fungsi f dan g dapat dikomposisikan sebagai f ◦ g jika range dari g merupakan himpunan bagian dari domain f.

Ini merupakan syarat komposisi fungsi.

Fungsi invers

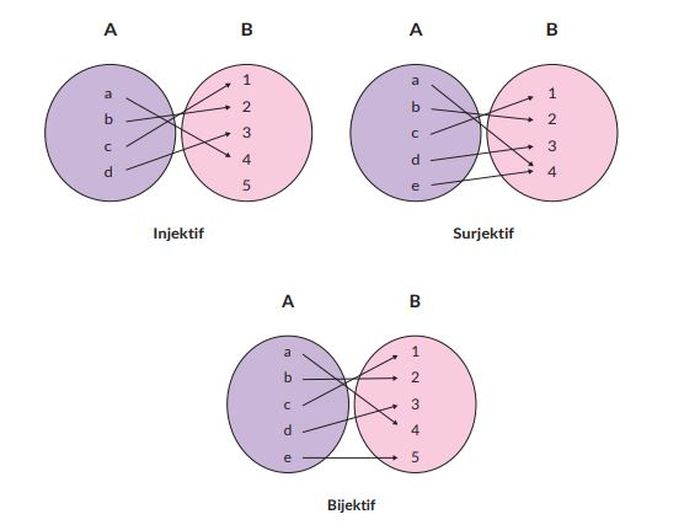
Fungsi invers sendiri dibagi menjadi tiga, yaitu fungsi injektif, surjektif, dan bijektif.

Lantas, fungsi seperti apa yang memiliki kebalikan atau invers? Secara umum tidak semua fungsi memiliki fungsi invers. Hanya fungsi bijektif (injektif dan surjektif) saja yang memiliki invers.

Agar lebih mudah memahaminya, siswa dapat melihat gambar di bawah ini.

Baca Juga: Kunci Jawaban Komposisi Fungsi Latihan 1.4 Halaman 30 Nomor 3-5 Matematika Kelas 11 SMA Kurikulum Merdeka

PROMOTED CONTENT