Nakita.id – Tak terasa bab 1 Matematika SMA kelas XI Kurikulum Merdeka sudah selesai.
Setelah membahas subbab demi subbab dan menjawab soal-soal latihan, seperti biasa Nakita akan memberikan rangkuman bab 1 tentang komposisi fungsi dan invers fungsi.
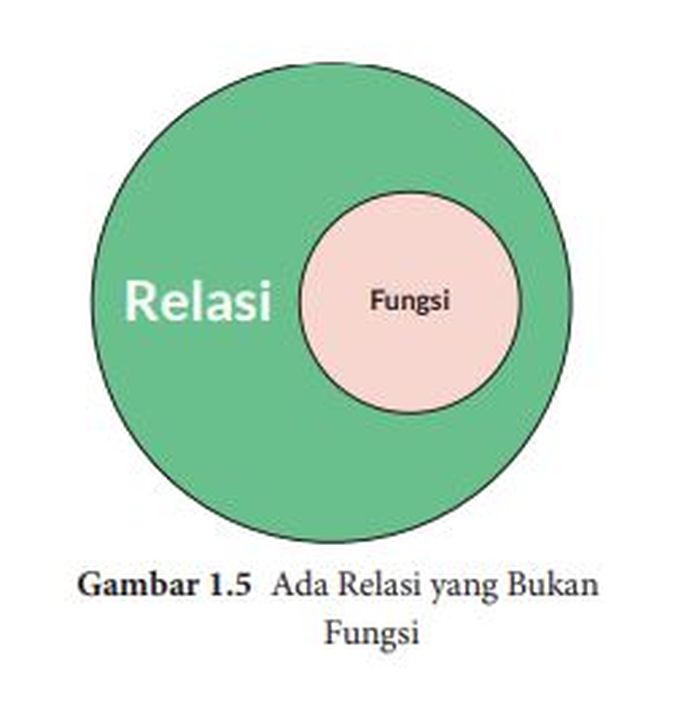
Relasi dapat dipahami dalam banyak hal di kehidupan sehari-hari. Konsep relasi menjelaskan hubungan antara anggota-anggota dari dua himpunan.
Contohnya, setiap pemain bola di tim Manchester United memiliki nomor punggung masing-masing. Ronaldo memiliki nomor punggung 7.
Hubungan ini biasanya dijelaskan dalam bentuk himpunan pasangan berurutan, diagram panah, dan diagram Kartesius.
Fungsi merupakan suatu relasi yang menghubungkan satu anggota dari suatu himpunan tepat ke satu anggota di himpunan yang lain. Fungsi adalah relasi yang lebih spesifik.
Fungsi biasa dinyatakan dalam bentuk f(x) = y , di mana f merupakan fungsi, x merupakan variabel masukan (input) dan y adalah variabel keluaran (output).
Agar lebih mudah memahami konsep ini, siswa dapat membayangkan fungsi sebagai mesin melalui gambar berikut ini:
Pada bagian ini, siswa akan belajar menentukan relasi-relasi yang merupakan fungsi dan bukan merupakan fungsi.
Relasi-relasi ini akan disajikan dalam bentuk diagram panah dan diagram Kartesius.
Baca Juga: Jawaban Lengkap Soal Fungsi Invers Latihan 1.5 Halaman 39 Matematika Kelas 11 SMA Kurikulum Merdeka
Relasi yang terdapat pada Gambar 1.6 (a) dan (b) merupakan fungsi karena relasi tersebut menghubungkan satu anggota himpunan input dengan tepat satu anggota himpunan output.
Gambar 1.6 (c) merupakan contoh relasi yang bukan fungsi karena relasi tersebut menghubungkan satu anggota; “q” ke dua anggota berbeda “y” dan “z” . Selain diagram, relasi juga sering ditampilkan dalam bentuk grafik.
Siswa dapat menentukan apakah relasi semacam ini merupakan fungsi atau bukan dengan menggunakan tes garis vertikal.
Caranya yaitu cukup menggeser garis vertikal dari kiri ke kanan (atau sebaliknya) dan melewati grafik relasi.
Apabila garis vertikal tersebut memotong grafik di dua atau lebih titik yang berbeda, maka relasi tersebut bukanlah fungsi.
Gambar A menampilkan grafik dari relasi dengan persamaan x = y2.
Dengan menggunakan tes garis vertikal, dapat dilihat bahwa pada x = 2 garis vertikal memotong grafik pada dua titik yang berbeda. Relasi ini bukanlah suatu fungsi.
Gambar B menampilkan grafik dari relasi dengan persamaan y = x3.
Dengan menggunakan tes garis vertikal, dapat dilihat bahwa untuk setiap nilai x, garis vertikal memotong grafik tepat pada satu titik.
Relasi ini adalah suatu fungsi.
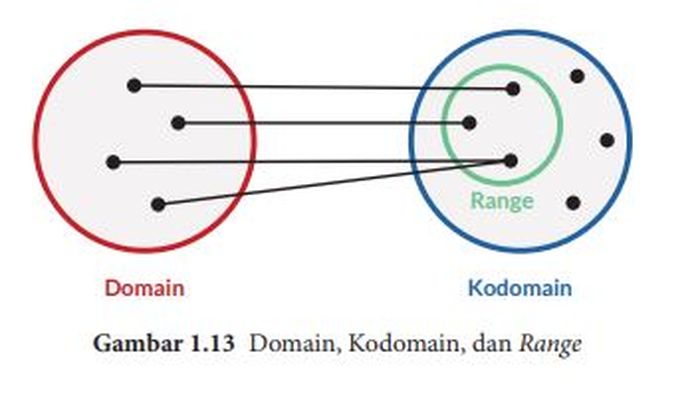
Di bangku SMP, domain, kodomain, dan range telah dipelajari sebelumnya.
Pengertian domain, kodomain, dan range dapat dilihat secara utuh dalam gambar di bawah ini.
Komposisi fungsi dibagi menjadi dua, yaitu penjumlahan dan pengurangan fungsi serta penjumlahan dan pengurangan fungsi.
Penjumlahan dua atau lebih fungsi dapat menghasilkan fungsi yang baru.
Jika f(x) dan g(x) merupakan dua fungsi dengan domain masing-masing Df dan Dg. Maka, penjumlahan (f + g) (x) = f (x) + g(x) menghasilkan fungsi yang baru dengan domain Df ∩ Dg.
Jika f(x) dan g(x) merupakan dua fungsi dengan domain masing-masing Df dan Dg. Maka, pengurangan (f − g)(x) = f(x) − g(x) menghasilkan fungsi yang baru dengan domain Df ∩ Dg.
Operasi penjumlahan dan pengurangan bisa diterapkan terhadap dua fungsi. Operasi ini bisa diperluas penerapannya untuk lebih dari dua fungsi.
Jika f(x) dan g(x) merupakan dua fungsi dengan domain masing-masing Df dan Dg. Maka, perkalian (f · g)(x) = f(x) · g(x) menghasilkan fungsi yang baru dengan domain Df ∩ Dg.
Pembagian dua fungsi (f/g) (x) = f(x)/g(x) secara umum belum tentu menghasilkan fungsi. Supaya f/g menjadi sebuah fungsi, pembagi g tidak boleh memiliki nilai 0. Dengan kata lain, f/g adalah fungsi dengan domain (Df ∩ Dg) – {x|g (x) = 0}.
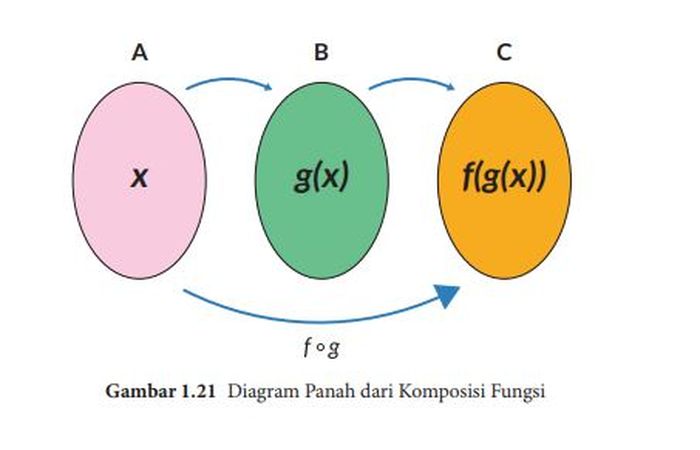
Jika g : A → B dan f : B → C merupakan dua fungsi, maka komposisi keduanya f (g (x)) dinyatakan dengan notasi (f ◦ g)(x) adalah fungsi dari domain A ke kodomain C.
Komposisi dua fungsi dapat dipahami melalui diagram panah berikut:
Dua fungsi f dan g dapat dikomposisikan sebagai f ◦ g jika range dari g merupakan himpunan bagian dari domain f.
Ini merupakan syarat komposisi fungsi.
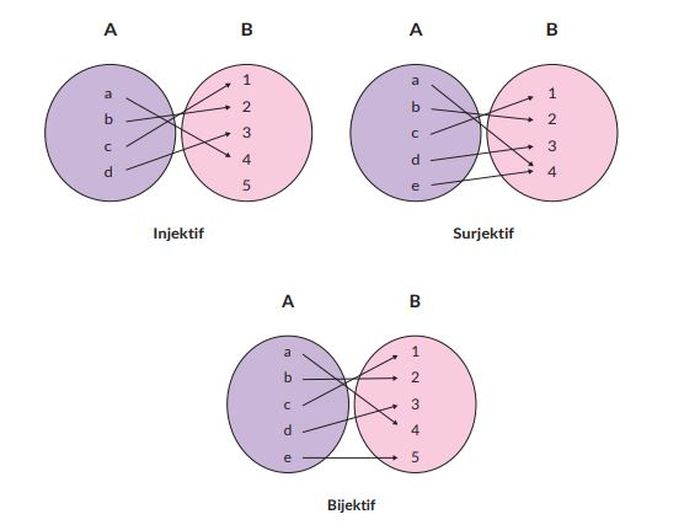
Fungsi invers sendiri dibagi menjadi tiga, yaitu fungsi injektif, surjektif, dan bijektif.
Lantas, fungsi seperti apa yang memiliki kebalikan atau invers? Secara umum tidak semua fungsi memiliki fungsi invers. Hanya fungsi bijektif (injektif dan surjektif) saja yang memiliki invers.
Agar lebih mudah memahaminya, siswa dapat melihat gambar di bawah ini.
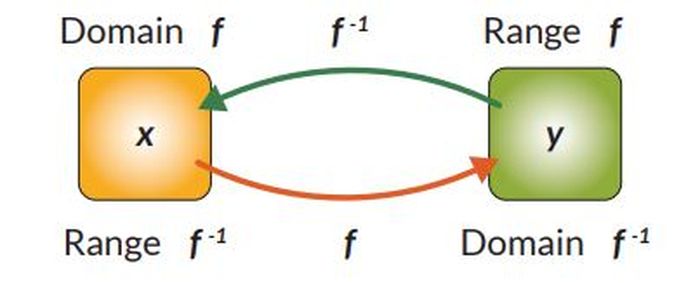
Fungsi yang berkebalikan operasinya dari fungsi asalnya disebut sebagai fungsi invers. Fungsi ini memetakan anggota yang ada di range fungsi asal ke anggota yang ada di domain fungsi asal.
Fungsi invers dituliskan sebagai f-1. Namun, perlu diingat bahwa −1 di sini bukan merupakan suatu pangkat.
Dari definisi fungsi invers yang baru dijelaskan sebelumnya, hubungan antara domain dan range dari fungsi asal dan fungsi invers dapat dipahami melalui diagram panah berikut.
Secara konsep, menentukan fungsi invers dari fungsi asal dengan diagram panah memang lebih intuitif; dengan membalik arah panah.
Namun, sering kali dijumpai bahwa fungsi asal dituliskan dalam bentuk persamaan matematis.
Dalam kasus ini, cara untuk menemukan persamaan fungsi invers dari fungsi asal dapat dilakukan dengan cara berikut:
1. Ubah y = f (x) menjadi bentuk x = f(y).
2. Ubah persamaan x = f(y) menjadi bentuk y = ... .
3. Ubahlah variabel y dengan f −1 (x) sehingga diperoleh rumus fungsi invers f −1 (x).
Nah, itu dia rangkuman bab 1 Matematika kelas 11 SMA Kurikulum Merdeka tentang komposisi fungsi dan fungsi invers. Semoga bermanfaat!
| Penulis | : | Aullia Rachma Puteri |
| Editor | : | Aullia Rachma Puteri |





KOMENTAR